Tutorial on using spatial SSAs in DiffEqJump
This blog will show how to use the functionality I added to DiffEqJump over the summer. See the documentation for a tutorial on getting started with DiffEqJump.
Installing DiffEqJump
To use DiffEqJump you will need to have julia installed. Once in REPL, do ] add DiffEqJump. After the installation finishes, you will be able to use all the functionality described below.
Reversible binding model on a grid
A 5 by 5 Cartesian grid:
| . | . | . | . | B |
| . | . | . | . | . |
| . | . | . | . | . |
| . | . | . | . | . |
| A | . | . | . | . |
Suppose we have a reversible binding system described by , where is the forward rate and is the backward rate. Further suppose that all molecules start in the lower left corner, while all molecules start in the upper right corner of a 5 by 5 grid. There are no molecules at the start.
We first create the grid:
using DiffEqJump
dims = (5,5)
num_nodes = prod(dims) # number of sites
grid = CartesianGrid(dims) # or use LightGraphs.grid(dims)Now we set the initial state of the simulation. It has to be a matrix with entry being the number of species at site (with the standard column-major ordering of the grid).
num_species = 3
starting_state = zeros(Int, num_species, num_nodes)
starting_state[1,1] = 25
starting_state[2,end] = 25
starting_stateWe now set the time-span of the simulation and the reaction rates. These can be chosen arbitrarily.
tspan = (0.0, 2.0)
rates = [3.0, 0.05] # k_1 = rates[1], k_2 = rates[2]Now we can create the DiscreteProblem:
prob = DiscreteProblem(starting_state, tspan, rates)Since both reactions are massaction reactions, we put them together in a MassActionJump. In order to do that we create two stoichiometry vectors. The net stoichiometry vector describes which molecules change in number and how much after each reaction; for example, [1 => -1] is the first molecule disappearing. The reaction stoichiometry vector describes what the reactants of each reaction are; for example, [1 => 1, 2 => 1] would mean that the reactants are one molecule of type 1 and one molecule of type 2.
netstoch = [[1 => -1, 2 => -1, 3 => 1],[1 => 1, 2 => 1, 3 => -1]]
reactstoch = [[1 => 1, 2 => 1],[3 => 1]]
majumps = MassActionJump(rates, reactstoch, netstoch)The last thing to set up is the hopping constants – the probability per time of an individual molecule of each species hopping from one site to another site. In practice this parameter, as well as reaction rates, are obtained empirically. Suppose that molecule cannot diffuse, while molecules and diffuse at probability per time 1 (i.e. the time of the diffusive hop is exponentially distributed with mean 1). Entry of hopping_constants is the hopping rate of species at site to any of its neighboring sites (diagonal hops are not allowed).
hopping_constants = ones(num_species, num_nodes)
hopping_constants[3, :] .= 0.0We are now ready to set up the JumpProblem with the next subvolume method.
alg = NSM() # Next Subvolume Method. Can also use DirectCRonDirect
jump_prob = JumpProblem(prob, alg, majumps, hopping_constants=hopping_constants, spatial_system = grid, save_positions=(true, false))The save_positions keyword tells the solver to save the positions just before the jumps. To solve the jump problem do
solution = solve(jump_prob, SSAStepper())Visualizing solutions of spatial jump problems is best done with animations.
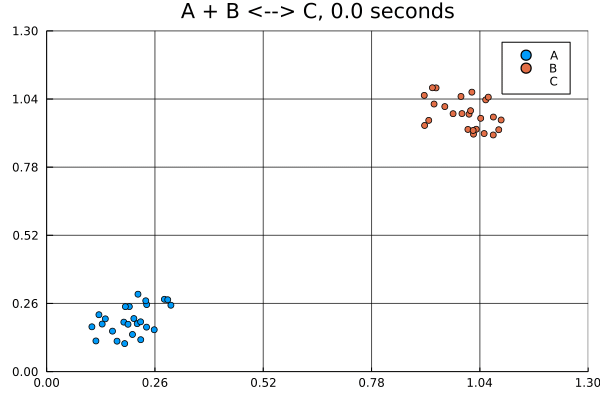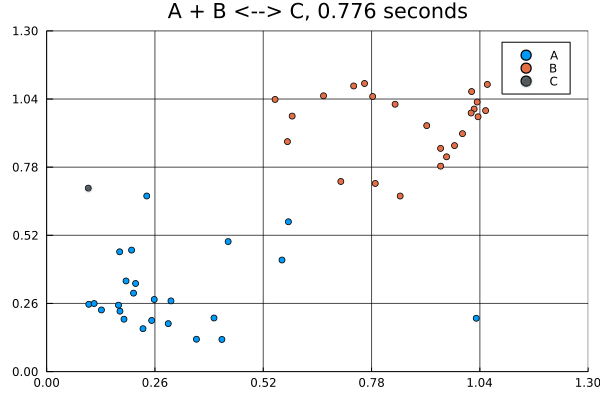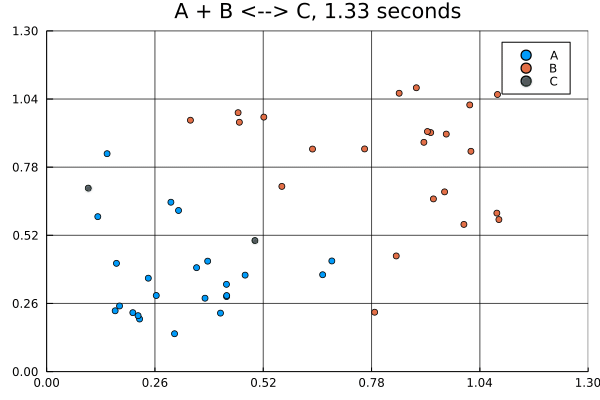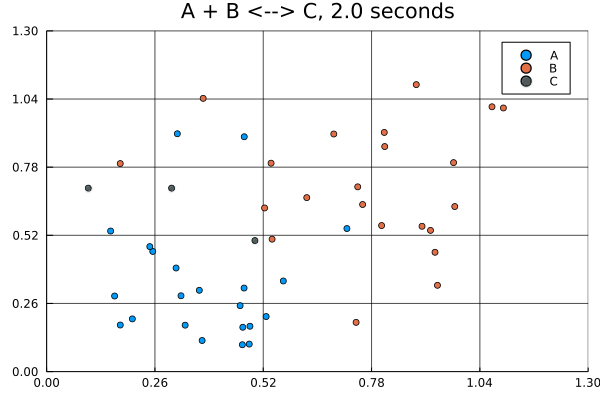
This animation was produced by this script.
Making changes to the model
Now suppose we want to make some changes to the reversible binding model above. There are three "dimensions" that can be changed: the topology of the system, the structure of hopping rates and the solver. The supported topologies are CartesianGrid – used above, and any AbstractGraph from LightGraphs. The supported forms of hopping rates are , and , where denotes the species, – the source site, and – the destination. The supported solvers are NSM, DirectCRDirect and any of the standard non-spatial solvers.
Topology
If our mesh is a grid (1D, 2D and 3D are supported), we can create the mesh as follows.
dims = (2,3,4) # can pass in a 1-Tuple, a 2-Tuple or a 3-Tuple
grid = CartesianGrid(dims)The interface is the same as for LightGraphs.grid. If we want to use an unstructured mesh, we can simply use any AbstractGraph from LightGraphs as follows:
using LightGraphs
graph = cycle_digraph(5) # directed cyclic graph on 5 nodesNow either graph or grid can be used as spatial_system in creation of the JumpProblem.
Hopping rates
The most general form of hopping rates that is supported is – each (species, source, destination) triple gets its own independent hopping rate. To use this, hopping_constants must be of type Matrix{Vector{F}} where F <: Number (usually F is Float64) with hopping_constants[s,i][j] being the hopping rate of species at site to neighbor at index . Note that neighbors are in ascending order, like in LightGraphs. Here is an example where only hopping up and left is allowed.
hopping_constants = Matrix{Vector{Float64}}(undef, num_species, num_nodes)
for ci in CartesianIndices(hopping_constants)
(species, site) = Tuple(ci)
hopping_constants[species, site] = zeros(outdegree(grid, site))
for (n, nb) in enumerate(neighbors(grid, site))
if nb < site
hopping_constants[species, site][n] = 1.0
end
end
endTo pass in hopping_constants of form we need two vectors – one for and one for . Here is an example.
species_hop_constants = ones(num_species)
site_hop_constants = Vector{Vector{Float64}}(undef, num_nodes)
for site in 1:num_nodes
site_hop_constants[site] = ones(outdegree(grid, site))
end
hopping_constants=Pair(species_hop_constants, site_hop_constants)We must combine both vectors into a pair as in the last line above.
Finally, to use in hopping_constants of form we construct a matrix instead of a vector for .
species_hop_constants = ones(num_species, num_nodes)
site_hop_constants = Vector{Vector{Float64}}(undef, num_nodes)
for site in 1:num_nodes
site_hop_constants[site] = ones(outdegree(grid, site))
end
hopping_constants=Pair(species_hop_constants, site_hop_constants)We can use either of the four versions of hopping_constants to construct a JumpProblem with the same syntax as in the original example. The different forms of hopping rates are supported not only for convenience but also for better memory usage and performance. So it is recommended that the most specialized form of hopping rates is used.
Solvers
There are currently two specialized "spatial" solvers: NSM and DirectCRDirect. The former stands for Next Subvolume Method and was previously described here. The latter employs Composition-Rejection to sample the next site to fire, similar to the ordinary DirectCR method. For larger networks DirectCRDirect is expected to be faster. Both methods can be used interchangeably.
Additionally, all standard solvers are supported as well, although they are expected to use more memory and be slower. They "flatten" the problem, i.e. turn all hops into reactions, resulting in a much larger system. For example, to use the Next Reaction Method (NRM), simply pass in NRM() instead of NSM() in the construction of the JumpProblem. Importantly, you must pass in hopping_constants in the D_{s,i,j} or D_{s,i} form to use any of the non-specialized solvers.
Animation script
using Plots
is_static(spec) = (spec == 3) # true if spec does not hop
"get frame k"
function get_frame(k, sol, linear_size, labels, title)
num_species = length(labels)
h = 1/linear_size
t = sol.t[k]
state = sol.u[k]
xlim=(0,1+3h/2); ylim=(0,1+3h/2);
plt = plot(xlim=xlim, ylim=ylim, title = "$title, $(round(t, sigdigits=3)) seconds")
species_seriess_x = [[] for i in 1:num_species]
species_seriess_y = [[] for i in 1:num_species]
CI = CartesianIndices((linear_size, linear_size))
for ci in CartesianIndices(state)
species, site = Tuple(ci)
x,y = Tuple(CI[site])
num_molecules = state[ci]
sizehint!(species_seriess_x[species], num_molecules)
sizehint!(species_seriess_y[species], num_molecules)
if !is_static(species)
randsx = rand(num_molecules)
randsy = rand(num_molecules)
else
randsx = zeros(num_molecules)
randsy = zeros(num_molecules)
end
for k in 1:num_molecules
push!(species_seriess_x[species], x*h - h/2 + h*randsx[k])
push!(species_seriess_y[species], y*h - h/2 + h*randsy[k])
end
end
for species in 1:num_species
scatter!(plt, species_seriess_x[species], species_seriess_y[species], label = labels[species], marker = 6)
end
xticks!(plt, range(xlim...,length = linear_size+1))
yticks!(plt, range(ylim...,length = linear_size+1))
xgrid!(plt, 1, 0.7)
ygrid!(plt, 1, 0.7)
return plt
end
"make an animation of solution sol in 2 dimensions"
function animate_2d(sol, linear_size; species_labels, title, verbose = true)
num_frames = length(sol.t)
anim = @animate for k=1:num_frames
verbose && println("Making frame $k")
get_frame(k, sol, linear_size, species_labels, title)
end
anim
end
# animate
anim=animate_2d(solution, 5, species_labels = ["A", "B", "C"], title = "A + B <--> C", verbose = false)
fps = 5
name = "ABC_anim_$(length(solution.u))frames_$(fps)fps.gif"
path = joinpath(name)
gif(anim, path, fps = fps)